Algebra v siedmej triede

Prvá epocha matematiky v 7.triede na waldorfských školách sa nesie v znamení algebraických výrazov. Z oblasti matematiky čísel sa dostávame do oblasti matematiky písmen. To, čo sme doteraz prežívali ako počítanie v rôznych oboroch čísel (do tohto obdobia žiaci zvládli celé čísla, zlomky, desatinné čísla a operácie s nimi) a rôzne pravidlá a mechanizmy, ktoré pri tom fungujú, nadobúdajú teraz charakter zovšeobecnení, až po jednotlivé matematické zákony.

Samozrejme, že sa na to ide pomaly, postupne. Je to predsa len určitý veľký krok, ktorý musia žiaci zvládnuť a je tu preto veľmi dôležitá zásada – menej je niekedy viac. Je dôležité dobre premyslieť kroky budovania učebnej látky tak, aby žiaci získali dobré základy pre neskoršie zložitejšie operácie.

A tak sa to celé začalo opakovaním vecí, ktoré už dávno vieme:

Znova si pripomenutie, že súčet si môžeme uľahčiť súčinom. A cez súčet a súčin sme sa dostali ku komutatívnemu zákonu, lebo 1+2=2+1 a rovnako to platí pre násobenie.

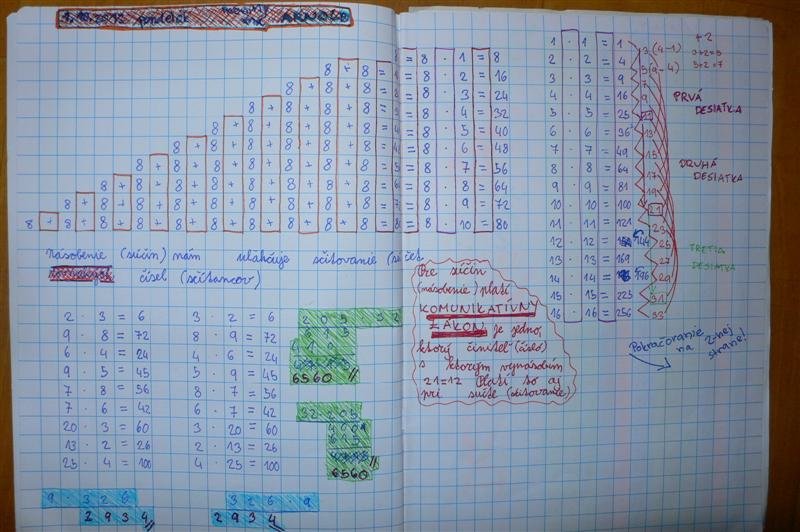
A od násobenia je to už len krok ku mocninám. 1x1=1=1na druhú

2x2=4=2na druhú....

A krok naspäť k tomu, z čoho sme začali, je prechod od sčítancov k činiteľom a pochopeniu mocnín:

2=2

2x2=4=2na druhú

2x2x2=8=2na tretiu.....

A do toho celého pamäťové počítanie na súčet rovnakých čísel, ako napríklad 2+2 a ďalší pridá k výsledku +2 a podobne s násobením až ku príkladom – myslím si číslo. Ak ho zväčším o 103, budem mať 125. Na aké číslo som myslela?

A ako si poradiť s násobením opúšťajúcim malú násobilku?

7x45=7x(40+5)=7x40+7x5=280+35=315

A sme pri roznásobovaní zátvoriek. Tejto téme predchádza príbeh. Máme manželov menom 12 a manželov menom 13. Idú na ples ale obe rodiny sú pohádané. A tak na plese tancuje manžel 10 z Dvanástkovej rodiny iba s manželkou z Trinástkovej rodiny a keďže je to veľmi veselý ples, tak aj s manželom od Trinástkovcov. Manželka od Dvanástkovcov s manželom od Trinástkovcov, ale aj s manželkou od trinástkovcov.

12x13=(10+2)x(10+3)=10x10+10x3+2x10+2x3=100+30+20+6=156

No a všetky možnosti tanečných párov sú pekne farebne vyznačené, aby sme na nikoho nezabudli.

A k zavedeniu premennej už je len krok, ale tomu predchádza veľa precvičovania a počítania písomne aj spamäti. Ak vieme nahradiť cifru premennou, vieme to postupne aj opačne a za premennú vieme dosadiť cifry a počítať potom rôzne výsledky. Príbeh k tejto téme bol ten, že naše manželské páry neboli na hociakom plese, ale na karnevale. A premenná je len maska, pod ktorou sa môže skrývať hociaká cifra, teda pán či pani Dvanástkovci, či hociktorí iní. Ale, keď sa odmaskujú a my už vieme, čo sú zač, tak vieme algebraický výraz aj vypočítať.

Okrem komutatívneho zákona sa popri týchto výpočtoch uplatňuje a teda aj preberie asociatívny a distributívny zákon, aby sme prácu so zátvorkami a ich roznásobovaním doviedli ku zovšeobecneniu.

A potom sa statočne precvičujú rôzne algebraické výrazy a ich výpočty a dosádzanie za premennú....

Ďalšia oblasť, ktorá k tejto téme patrí, aby sme sa mohli dostať k rovniciam, je obor záporných čísel. K tým sme sa dostali cez rozpočet v domácnosti. Tu sme si pospomínali na ekonomickú matematiku zo šiesteho ročníka. Čo to znamená vyrovnaný rozpočet, ako sa dá aj šetriť, a čo sa stane, ak máme málo? Dlhy sú to, kde sa dá najlepšie vysvetliť záporné číslo a ako sa s ním pracuje. Na peniaze sme citliví všetci a naše deti nie sú výnimkou. Čo to znamená nemať, už dobre poznajú, aj keď za nich ich dlhy splácajú ešte ich rodičia. Teda, žiadne také, že ak sčituješ kladné čísla, je to plus, ak záporné mínus... Ale, čo to znamená, keď si v pluse a ešte ti pribudne? Čo to znamená, keď si v pluse, ale chceš minúť viac ako máš? A až po tom sa dostávame k absolútnym hodnotám, aby sme si mohli vyvodiť závery – pravidlá pre počítanie so zápornými číslami.

V tejto časti sme sa venovali len súčtu a rozdielu súčin a podiel nás bude čakať pred zavedením rovníc.

Vyskúšali sme si aj samostatnú prácu s príkladmi zo štátnych škôl a samostatnú prácu so samokontrolou.

Aby boli zošity krásne, tak na to sa vo waldorfskej škole snažíme dbať. Každý robí koľko vládze a pojme to podľa seba.

To, čo bolo pri matematike dôležité, bolo – od zážitku k poučke, k definícii, k zákonu. A - veľa humoru. Ak ho pri pubertiakoch stratíte, stratili ste všetko. V ich svete vás nič iné ako nadhľad a smiech nezachráni.